Fatigue is the repeated loading and unloading of metal due to direct load variation or eccentricity in a rotating shaft, or differential thermal expansion of a structure. Even substantially below the yield point (elastic limit) of a metal or alloy this repeated loading can lead to failure, usually measured in terms of the number of cycles (repeated load applications) to failure. Some studies have suggested that well over 80% of all mechanical failures of metal are attributable to fatigue.

High-stress, low-cycle fatigue usually occurs at stresses above the yield point and lifetimes are tens or hundreds of cycles (to about a thousand cycles). Failure occurs as a result of the accumulation of plastic deformation, that is, the area (energy) under the stress–strain curve. A simple lifetime predictive equation can be used to predict lifetime:

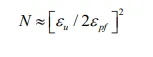
where N is the number of cycles to failure, εu is total strain from the stress–strain curve, and εpf is the plastic strain amplitude in each fatigue cycle. More commonly, metals are used well below their yield point and fail after many cycles of repeated loading in lowstress, high-cycle fatigue. Early in the fatigue process surface flaws or in some cases severe internal flaws begin to propagate. The fatigue crack propagation in areas of high stress has a small distance with each tensile loading. The propagation on each cycle frequently leaves identifiable marking on the failure surface termed fatigue striations which mark the progress of the subcritical crack. When the crack becomes so large than the fracture toughness criterion, the catastrophic overload failure occurs.

Figure 4 shows typical metal S–N curves (stress vs. number of cycles to failure) for a high- strength aluminum and for a titanium alloy.

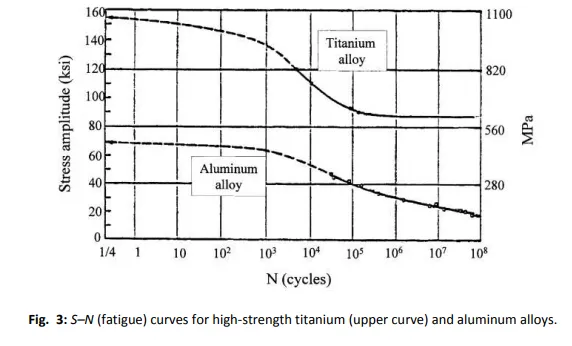
Note that the convention is to make stress the vertical axis and to plot the number of cycles to failure on a logarithmic scale. For high-stress, low-cycle fatigue

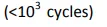
the curve is flat and linear, consistent with the model of Equation 3. For high cycle fatigue the lifetime is a rapidly varying function of stress until very low stresses (long lifetimes occur). A number of mathematical relationships have been proposed to predict fatigue life, but none works with complete success and all require experimental data. Perhaps the most successful of the so-called “fatigue “laws” are the “cumulative damage” laws. The simplest is Miner’s law:

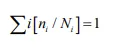
where ni is the number of cycles applied and Ni is the number of cycles for failure at a particular stress level, σi . The conceptual basis is that the number of fatigue cycles at a stress level may be correlated to fatigue crack propagation.