Continuum mechanics is essentially based on fundamental principles having the character of axioms, that are laws, which cannot be proven but are commonly assumed to be true. In his “Philosophiae Naturalis Principia Mathematica” of 1687, ISAAC NEWTON established laws of motion und thus was the first relating kinematical and dynamic quantities. Without applying mathematical equations at that time, they read as follows:

Brought into a more modern and mathematical form, they still constitute the fundament of NEWTONian mechanics. In particular, the first one states that the laws of motion are only valid for an inertial reference frame (see section 4.6). The second law is the balance of (linear) momentum and the third is the reaction principle of eq. (5.5).
General Balance Equation
The axioms of continuum mechani cs are formulated as balance laws or conservation laws for mechanical quantities like mass, momentum, energy etc. and established as equations of integrals over a material body (global form), or as field equations (local form). They are material independent and applicable to all continua, regardless of their internal physical structure. These fundamental equations will be formulated in their spatial (EULERean) form, which means that all field quantities are expressed as functions of the coordinates of a material point in the actual configuration. As time derivatives of the integrals will be required, they are transformed to the reference configuration ((LAGRANGEan form), differentiated under the integral and transformed back to the EULERean description, again. time derivatives of integrals over material volumes or surfaces in the actual configuration. By this procedure of exchanging the integration and differentiation process, the local field equation is obtained from a global balance law.



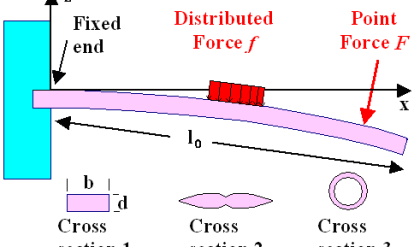
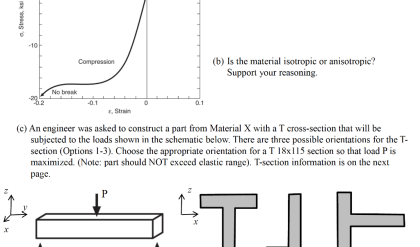

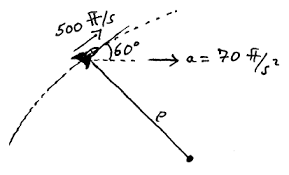

Comments are closed.