Introduction
Continuum mechanics is concerned with motion and deformation of material objects, called bodies, under the action of forces. If these objects are solid bodies, the respective subject area is termed solid mechanics, if they are fluids, it is fluid mechanics or fluid dynamics. The mathematical equations describing the fundamental physical laws for both solids and fluids are alike, so the different characteristics of solids and fluids have to be expressed by constitutive equations. Obviously, the number of different constitutive equations is huge considering the large number of materials. All of this can be written using a unified mathematical framework and common tools. In the following we concentrate on solids. Continuum mechanics is a phenomenological field theory based on a fundamental hypothesis called continuum hypothesis. The governing equations comprise material independent principles, namely
· Kinematics, being a purely geometrical description of motion and deformation of material bodies;
· Kinetics, addressing forces as external actions and stresses as internal reactions;
· Balance equations for conservation of mass, momentum and energy; and material dependent laws, the
· Constitutive equations. Altogether, these equations form an initial boundary value problem.
Notion and Configuration of a Continuum
It is commonly known, that matter consists of elementary particles, atoms and molecules, which are small but finite and not homogeneously distributed. The mechanical behaviour of materials is determined by the interaction of these elementary constituents. However, an engineering modelling cannot be done at this level and length scale. Even on a next higher length scale, the microstructure of materials appears as inhomogeneous and consisting of different constituents. Again, if one is interested in the macroscopic behaviour of an engineering structure, modelling on a microscopic length scale is in general not feasible. While studying the external actions on objects, it will, except for specific questions concerning the relations between micro- and macroscopic properties, not be necessary to account for the non-homogeneous microstructure. The discretely structured matter will hence be represented by a phenomenological model, the continuum, by averaging its properties in space and neglecting any discontinuities and gaps. By a continuum, we mean the hypothetical object in which the matter is continuously distributed over the entire object. It does not contain any intrinsic length scale.
The concept of a continuum is deduced from mathematics, namely the system of real numbers: between any two distinct real numbers there is always another distinct real number, and therefore, there are infinitely many real numbers between any two distinct numbers. The three-dimensional (EUKLIDean) space is a continuum of points, which can be represented by three real numbers, the coordinates, xi (i = 1, 2, 3). The same holds for the physical time, t, which can also be represented by a real number, and thus time and space together form a four-dimensional continuum.
Following is a description Albert EINSTEIN gave on p. 83 of his Relativity; The Special and the General Theory: The surface of a marble table is spread out in front of me. I can get from any one point on this table to any other point by passing continuously from one point to a “neighbouring” one, and repeating this process a (large) number of times, or, in other words, by going from point to point without executing “jumps”. I am sure the reader will appreciate with sufficient clearness what I mean here by “neighbouring” and by “jumps” (if he is not too pedantic). We express this property of the surface by describing the latter as a continuum.

This one-to-one correspondence allows us to speak of points, lines, surfaces and volumes in a continuum. For simplicity, material points, material surfaces and material bodies are often referred to as points, surfaces and volumes. The above definition is commonly supplemented by three characteristics, which are introduced axiomatically.
(1) A material continuum remains a continuum under the action of forces. Hence, two particles that are neighbours at one time remain neighbours at all times. We do allow bodies to be fractured, but the surfaces of fracture must be identified as newly created external surfaces.
(2) Stresses and strains can be defined everywhere in the body, i.e. they are field quantities.
(3) The theory of “simple materials” postulates, that the stress at any point in the body depends only on the deformation history of that very point but not on the deformation history of other points of the body. This relation may be affected by other physical quantities, such as temperature, but these effects can be studied separately. This is of course a greatly simplifying assumption, which facilitates the establishing of constitutive relations on the one hand but restricts their generality.
A scalar field describes a one-to-one correspondence between a single scalar number and the value of a physical quantity. A triple of numbers can be assigned to a geometric point, representing its coordinates, but also to any other physical quantity characterised by a magnitude and an orientation, i.e. a vector. A 33 matrix of numbers can be assigned to a tensor of rank two, if these numbers obey certain transformation rules. Within this concept, scalar fields may be referred to as tensor fields of rank or order zero, whereas vector fields are called tensor fields of rank or order one. Generally, tensors have certain invariant properties, i.e. properties, which are independent of the coordinate system used to describe them. Because of this attribute, we can use tensors for representing various fundamental laws of physics, which are supposed to be independent of the coordinate systems considered Finally, every function of space and time considered in the following is supposed to be differentiable up to any desired order in the region of interest.
Density and Mass

Continuum Hypothesis
Introduction
Continuum mechanics is concerned with motion and deformation of material objects, called bodies, under the action of forces. If these objects are solid bodies, the respective subject area is termed solid mechanics, if they are fluids, it is fluid mechanics or fluid dynamics. The mathematical equations describing the fundamental physical laws for both solids and fluids are alike, so the different characteristics of solids and fluids have to be expressed by constitutive equations. Obviously, the number of different constitutive equations is huge considering the large number of materials. All of this can be written using a unified mathematical framework and common tools. In the following we concentrate on solids. Continuum mechanics is a phenomenological field theory based on a fundamental hypothesis called continuum hypothesis. The governing equations comprise material independent principles, namely
· Kinematics, being a purely geometrical description of motion and deformation of material bodies;
· Kinetics, addressing forces as external actions and stresses as internal reactions;
· Balance equations for conservation of mass, momentum and energy; and material dependent laws, the
· Constitutive equations. Altogether, these equations form an initial boundary value problem.
Notion and Configuration of a Continuum
It is commonly known, that matter consists of elementary particles, atoms and molecules, which are small but finite and not homogeneously distributed. The mechanical behaviour of materials is determined by the interaction of these elementary constituents. However, an engineering modelling cannot be done at this level and length scale. Even on a next higher length scale, the microstructure of materials appears as inhomogeneous and consisting of different constituents. Again, if one is interested in the macroscopic behaviour of an engineering structure, modelling on a microscopic length scale is in general not feasible. While studying the external actions on objects, it will, except for specific questions concerning the relations between micro- and macroscopic properties, not be necessary to account for the non-homogeneous microstructure. The discretely structured matter will hence be represented by a phenomenological model, the continuum, by averaging its properties in space and neglecting any discontinuities and gaps. By a continuum, we mean the hypothetical object in which the matter is continuously distributed over the entire object. It does not contain any intrinsic length scale.
The concept of a continuum is deduced from mathematics, namely the system of real numbers: between any two distinct real numbers there is always another distinct real number, and therefore, there are infinitely many real numbers between any two distinct numbers. The three-dimensional (EUKLIDean) space is a continuum of points, which can be represented by three real numbers, the coordinates, xi (i = 1, 2, 3). The same holds for the physical time, t, which can also be represented by a real number, and thus time and space together form a four-dimensional continuum.
Following is a description Albert EINSTEIN gave on p. 83 of his Relativity; The Special and the General Theory: The surface of a marble table is spread out in front of me. I can get from any one point on this table to any other point by passing continuously from one point to a “neighbouring” one, and repeating this process a (large) number of times, or, in other words, by going from point to point without executing “jumps”. I am sure the reader will appreciate with sufficient clearness what I mean here by “neighbouring” and by “jumps” (if he is not too pedantic). We express this property of the surface by describing the latter as a continuum.

This one-to-one correspondence allows us to speak of points, lines, surfaces and volumes in a continuum. For simplicity, material points, material surfaces and material bodies are often referred to as points, surfaces and volumes. The above definition is commonly supplemented by three characteristics, which are introduced axiomatically.
(1) A material continuum remains a continuum under the action of forces. Hence, two particles that are neighbours at one time remain neighbours at all times. We do allow bodies to be fractured, but the surfaces of fracture must be identified as newly created external surfaces.
(2) Stresses and strains can be defined everywhere in the body, i.e. they are field quantities.
(3) The theory of “simple materials” postulates, that the stress at any point in the body depends only on the deformation history of that very point but not on the deformation history of other points of the body. This relation may be affected by other physical quantities, such as temperature, but these effects can be studied separately. This is of course a greatly simplifying assumption, which facilitates the establishing of constitutive relations on the one hand but restricts their generality.
A scalar field describes a one-to-one correspondence between a single scalar number and the value of a physical quantity. A triple of numbers can be assigned to a geometric point, representing its coordinates, but also to any other physical quantity characterised by a magnitude and an orientation, i.e. a vector. A 33 matrix of numbers can be assigned to a tensor of rank two, if these numbers obey certain transformation rules. Within this concept, scalar fields may be referred to as tensor fields of rank or order zero, whereas vector fields are called tensor fields of rank or order one. Generally, tensors have certain invariant properties, i.e. properties, which are independent of the coordinate system used to describe them. Because of this attribute, we can use tensors for representing various fundamental laws of physics, which are supposed to be independent of the coordinate systems considered Finally, every function of space and time considered in the following is supposed to be differentiable up to any desired order in the region of interest.
Density and Mass


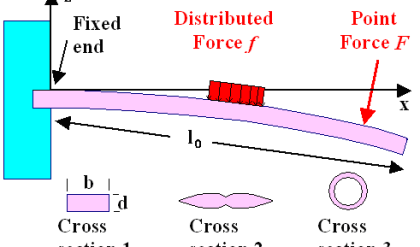
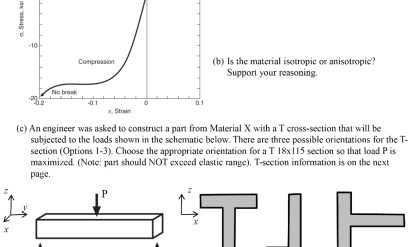

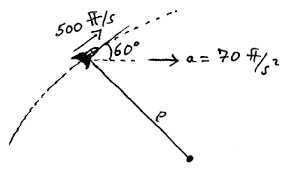
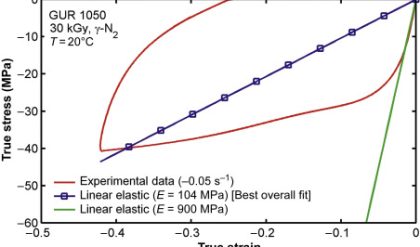
Comments are closed.